Test di Student: che cos’è e dove si applica veramente

Conoscere come applicare il test di Student può essere importante per il mercato del lavoro attuale. Perché le aziende non hanno più tempo o voglia di filosofeggiare, la crisi ha asciugato le possibilità di perdere tempo, ed ora lo spazio s’è ridotto a chi sa davvero mettere sul tavolo delle competenze lavorative specialistiche. Lo sa bene una realtà come l’università Niccolò Cusano che vuole darvi solo formazione spendibile e, quindi, si impegna a studiare corsi di laurea e master in grado di trasferire know-how specialistico. Se i numeri vi appassionano e credete che sia interessante per le vostre prospettive future lavorare nel campo della statistica, ecco una mini-guida in grado di darvi quella scintilla da cui potrebbe “accendersi” un impiego migliore. Buona lettura.

Maneggiare coi numeri è utile. Farlo da esperti di statistica ancor di più. Se questo è il vostro campo, capiamolo insieme iniziando a testare il terreno su cui andresti a muovervi. Vediamo se capite le idee chiave ed il funzionamento del test di Student.

La premessa del test T di Student è che si potrebbe avere la necessità di confrontare due medie. Ci vogliono, in buona sostanza, esperti in grado di asserire, in modo scientifico, che una eventuale differenza  riscontrata tra due medie analizzate non sia causata dal fato ma da una vera  diversità tra le medie delle due popolazioni da cui i campioni stessi derivano. Detto in modo più prosaico: dovrete poter affermare che due campioni analizzati appartengano a popolazioni diverse riguardo alla variabile considerata. Questa immagine ben illustra quanto detto:

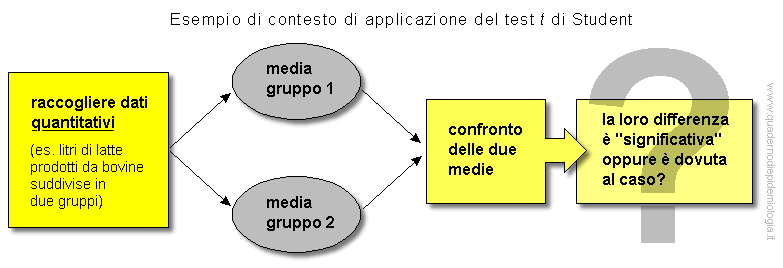
Lo schema di ragionamento del test T è questo mostrato nell’immagine:

I calcoli da eseguire per effettuare il test t sono un po’ complesso. Per pura completezza dell’informazione, la formula di calcolo del valore T:

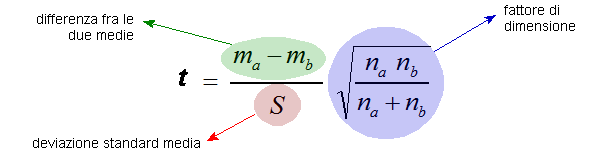
Il principio che “sta dietro” al calcolo del test T di Student va colto nella sua interezza ma bisogna anche dire il test t si svolge al computer con l’aiuto di apposito software, incluso in pacchetti statistici oppure reperibile in rete. Diversa, invece, è la preparazione accademica e post laurea che serve per usare al meglio questi strumenti. Uncinammo vi offre corsi di laurea in Economia davvero ben fatti ed anche corsi post laurea pensati per darvi strumenti da usare con le aziende. Un esempio per tutti? Il master di primo livello in “Data analyst” chi vi invitiamo a scoprire. In generale, potrete usufruire della preziosa scelta di quale formazione usare di più tra la FAD (Formazione a Distanza) e la FIP (Formazione in Presenza) in base alle difficoltà delle singole materie e ai vostri impegni di vita.

T di Student

Per meglio comprendere questo concetto denso del T di Student vi proponiamo un esempio di applicazione del test T. State sperimentando l’effetto sul suino dell’aggiunta alla razione di una miscela probiotica costituita da batteri normalmente presenti nella flora intestinale del suino. L’ipotesi da verificare è che il probiotico favorisca l’accrescimento degli animali.

Allo scopo di verificare l’ipotesi, avete disegnato uno studio statistico sperimentale preliminare su due piccoli gruppi di suini. I gruppi sono fra loro omogenei (stessa razza, età, provenienza ecc.) e sono mantenuti nelle stesse condizioni di allevamento (alimentazione, temperatura ambiente ecc.). L’unica differenza è che alla razione del Gruppo 1 (10 suini) viene aggiunto il probiotico, mentre al gruppo 2 (11 suini) no.

All’inizio dell’esperimento ciascun suino viene pesato; dopo 21 giorni di trattamento i suini vengono pesati di nuovo e per ogni animale si calcola l’incremento giornaliero medio. I dati (fittizi) sono riportati nella tabella che segue.

Imparando a confrontare le medie degli accrescimenti, potete notare che il valore del Gruppo 1 è superiore a quello del Gruppo 2 (643.8 g/giorno contro 637.0 g/giorno). La domanda è: questa differenza è dovuta al probiotico oppure al caso? L’ipotesi zero dice che la differenza è dovuta al caso. Accettate o rifiutate questa ipotesi? Per rispondere, potete applicare ai vostri dati il test T.

La tabella T Student

Il test di Student ha precisi margini di applicazione. Capire i contorni della tabella significa capire come muoversi al meglio. Ritornando all’esempio di sopra, potete senza problemi applicare il test T, magari utilizzando questo foglio di calcolo. Facendo così, otterrete un valore pari a 2.2796.

Ed ora? Confrontate il valore T che avete ottenuto (2.2796) con quelli presenti nella Tabella dei valori t, per 19 gradi di libertà (gradi di libertà=numero osservazioni-numero gruppi; nel nostro esempio 21-2=19). Il vostro valore è superiore a quello della colonna p=5% (ma inferiore a quello della colonna p=1%). Perciò potete rifiutare l’ipotesi zero e concludere che la differenza è significativa per p<0.05 (ma non per p<0.01). Questo vuol dire che c’è una probabilità inferiore al 5% (ma non all’1%) che la differenza di accrescimento tra il gruppo trattato e quello di controllo sia dovuta al caso.

Ora avete le basi per muovervi col test di Student ma, soprattutto, avete le basi per capire se quello della Statistica è il vostro mondo, fatevi ulteriormente un’idea andando più a fondo sul tema in rete o, meglio, leggendo gli articoli che con quotidianità mettiamo nel nostro blog universitario della città di Catania. Domande e dubbi, invece, li potete estrinsecare attraverso l’apposito form di richiesta.